Calcul de la racine carrée.

Il existe plusieurs algorithmes pour calculer la racine carrée d'un nombre positif. En voici deux:

1) Sachant que calculer la racine carrée de a revient à résoudre l'équation x2=a. On peut transformer celle-ci en:
x2=a Û 2 x2= x2 + a Û x = (x2 + a)/(2x) Û x = (x + a/x)/2
L'idée de génie (de qui?) a été de distinguer les x suivant les membres où ils se trouvaient pour donner la formule:

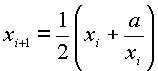
En faisant cela, on retrouvait la formule de Newton (ou formule de la tangente) qui affirme que dans le cas présent, le nombre de chiffres significatifs est au moins doublé à chaque calcul.

NOTE: le calcul peut commencer avec n'importe quelle valeur de x (différente de 0).

Exemple: x2=2 
x0=1 
x1=0.5*(1+2/1)=3/2=1.5
x2=0.5*(1.5+2/1.5)=17/12=1.4166666
x2=0.5*(1.416666+2/1.416666)=577/408=1.41421568
....
2) Voici un autre algorithme qui calcule la racine carrée d'un nombre réel a:
Exemple: a=543,21 
On écrit ce nombre par tranche de deux (en partant de la virgule) 5 43 , 21 00
Du premier groupe, on soustrait les premiers nombres impairs : 5-1-3=1.
Comme nous avons effectué 2 soustractions, le premier chiffre est un 2.
On recommence avec 143 (le reste des soustractions suivi du deuxième groupe) dont on soustrait les impairs à partir de 41 (dernier impair utilisé augmenté de 1 puis multiplié par 10 et augmenté de 1) : 143-41-43-45=14
La racine approchée est donc 23 (puisqu’il y a eu 3 soustractions)
On recommence avec 1421 (le reste des soustractions suivi du groupe suivant) dont on soustrait les impairs à partir de 461 (dernier impair utilisé augmenté de 1 puis multiplié par 10 et augmenté de 1) : 1421-461-463-465=34
La racine approchée est donc 23,3 (puisqu’il y a eu 3 soustractions)
On recommence avec 3400 (le reste des soustractions suivi du groupe suivant) dont on soustrait les impairs à partir de 4661 (dernier impair utilisé augmenté de 1 puis multiplié par 10 et augmenté de 1) : 3400-4661 est négatif!
La racine approchée est donc 23,30 (puisqu’il y a eu 0 soustraction)

PROGRAM RACINE;

VAR x,x2,Rac:REAL;
    i,N,Cpt,N_Dec,PartieEntiere,Divi:LONGINT;

BEGIN
WRITE('Introduisez le nombre dont il faut calculer la racine: ');
READLN(x);
x:=ABS(x);(* Pour le rendre positif *)
x2:=x;    (* Sauvegardé pour l'affichage final *)
(* Calcul du 1er chiffre - Aurait pu se faire par les logarithmes *)
PartieEntiere:=TRUNC(x);
N:=PartieEntiere;
Divi:=1;
WHILE NOT (N=0) DO
  BEGIN
  Divi:=Divi*100;
  N:=N DIV 100;
  END;
Divi:=Divi DIV 100;
N:=PartieEntiere DIV Divi;           (* La tranche la plus à gauche *)
PartieEntiere:=PartieEntiere-N*Divi; (* Les autres chiffres *)
i:=1;                                (* i contient les nombres impairs successifs *)
Cpt:=0;                              (* Cpt compte les soustractions *)
WHILE NOT (N-i<0) DO
  BEGIN
  N:=N-i;
  INC(Cpt);
  INC(i,2);
  END;
Rac:=Cpt;                            (* 1er chiffre *)
DEC(i,2);
(* Calcul des autres chiffres de la partie entière *)
Divi:=Divi DIV 100;
WHILE NOT (Divi=0) DO
  BEGIN
  N:=N*100+PartieEntiere DIV Divi;
  i:=(i+1)*10+1;
  Cpt:=0;
  WHILE NOT (N-i<0) DO
    BEGIN
    N:=N-i;
    INC(i,2);INC(Cpt);
    END;
  DEC(i,2);
  Rac:=Rac*10+Cpt;
  PartieEntiere:=PartieEntiere-(PartieEntiere DIV Divi)*Divi;
  Divi:=Divi DIV 100;
  END;
(* Calcul des chiffres de la partie décimale *)
x:=x-TRUNC(x);
Divi:=10;
N_Dec:=6;(* N_Dec = nombre de décimales *)
WHILE NOT (N_Dec=0) DO
  BEGIN
  N:=N*100+TRUNC(x*100);
  i:=(i+1)*10+1;
  Cpt:=0;
  WHILE NOT (N-i<0) DO
    BEGIN
    N:=N-i;
    INC(i,2);INC(Cpt);
    END;
  DEC(i,2);DEC(N_Dec);
  Rac:=Rac+Cpt/Divi;WRITELN(Rac:9:6);
  x:=x-TRUNC(x*100);Divi:=Divi*10;
  END;
WRITELN('Valeur par l''algo:',Rac:10:3);
WRITELN('Valeur par SQRT:',SQRT(x2):10:3);
READLN;
END.
Page précédente.
Page d'accueil.