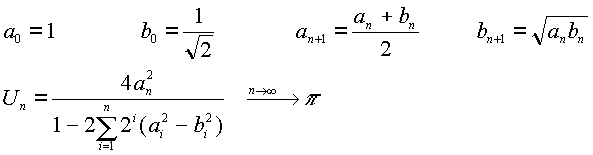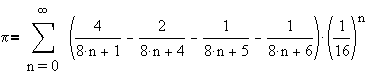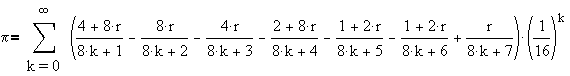A propos de pi.
Le nombre  est à beaucoup de titres
un nombre magique et depuis plus de 4 mille ans, il exacerbe la curiosité
des mathématiciens.
est à beaucoup de titres
un nombre magique et depuis plus de 4 mille ans, il exacerbe la curiosité
des mathématiciens.
Il semble qu'il soit connu depuis longtemps que le rapport de la
circonférence d'un cercle et de son diamètre soit constant.
Ceci n'implique pas pour autant que ce rapport ait été
associé à un nombre particulier. En effet, la notion du nombre
 n'apparaît qu'au XVIIe siècle
et l'usage de la lettre grecque qui commence avec le gallois William Jones
en 1706 (il lui attribue la valeur 3,14159) ne se répandra vraiment
qu'après avoir été employée par Euler en
1737.
n'apparaît qu'au XVIIe siècle
et l'usage de la lettre grecque qui commence avec le gallois William Jones
en 1706 (il lui attribue la valeur 3,14159) ne se répandra vraiment
qu'après avoir été employée par Euler en
1737.
Notons que seuls les nombres  , e et i ont droit
à une lettre pour les représenter. A titre indicatif,
il est amusant de souligner la relation 1+ei
, e et i ont droit
à une lettre pour les représenter. A titre indicatif,
il est amusant de souligner la relation 1+ei =0
qui unit ces 3 nombres.
=0
qui unit ces 3 nombres.
Rappelons que i est le nombre complexe tel que i2=-1.
Une des premières apparitions d'une valeur de  se trouve dans
une liste de spécifications concernant la construction du temple de
Salomon, aux environs de 950 avant J.C. et elle vaut 3. Cette valeur manque
évidemment de précision mais du temps des Egyptiens et
Mésopotamiens, de meilleures estimations avaient déjà
cours, à savoir 25/8 = 3,125 et
se trouve dans
une liste de spécifications concernant la construction du temple de
Salomon, aux environs de 950 avant J.C. et elle vaut 3. Cette valeur manque
évidemment de précision mais du temps des Egyptiens et
Mésopotamiens, de meilleures estimations avaient déjà
cours, à savoir 25/8 = 3,125 et
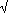 10 = 3,162. On
retrouve aussi trace de rapport circonférence/diamètre
dans la Bible où on lui attribue la valeur 3.
10 = 3,162. On
retrouve aussi trace de rapport circonférence/diamètre
dans la Bible où on lui attribue la valeur 3.
Le Papyrus Rhind cite pour  la valeur de
256/81=4*(1-1/9)2=3,16049...
la valeur de
256/81=4*(1-1/9)2=3,16049...
Rappelons que ce papyrus est la copie faite vers 1650 avant J.C. d'un
texte encore plus ancien et que la valeur de  n'apparaissait
pas telle qu'écrite ci-dessus puisque les expressions
algébriques étaient inconnues et que toute technique de
résolution était exprimée en langage habituel. Cette
expression est la déduction d'une règle permettant de calculer
l'aire d'un cercle à partir de son rayon.
n'apparaissait
pas telle qu'écrite ci-dessus puisque les expressions
algébriques étaient inconnues et que toute technique de
résolution était exprimée en langage habituel. Cette
expression est la déduction d'une règle permettant de calculer
l'aire d'un cercle à partir de son rayon.
En utilisant des propriétés géométriques,
et plus près de nous (mais tout est relatif), Archimède de
Syracuse (287-212 avant J.C.) encadra le cercle par des polygones inscrits
et circonscrits pour en arriver à 223/71< <22/7.
Avec l'affinement des techniques de calcul mais en se basant toujours sur
l'encadrement d'Archimède, Ptolémée trouva au IIe
siécle après J.C. la valeur sexagésimale
3+8/60+30/3600=3,141666... Vers 500, Aryabhatta utilise 62832/2000=3,1416.
Au XVIe siècle, 30 décimales sont connues, 140 au
XVIIIe et 707 par Shanks à la fin du XIXe
(mais plus de 200 étaient fausses).
<22/7.
Avec l'affinement des techniques de calcul mais en se basant toujours sur
l'encadrement d'Archimède, Ptolémée trouva au IIe
siécle après J.C. la valeur sexagésimale
3+8/60+30/3600=3,141666... Vers 500, Aryabhatta utilise 62832/2000=3,1416.
Au XVIe siècle, 30 décimales sont connues, 140 au
XVIIIe et 707 par Shanks à la fin du XIXe
(mais plus de 200 étaient fausses).
La course à la recherche du plus grand nombre de décimales
de  ne date bien sûr pas d'aujourd'hui mais l'utilisation
de l'ordinateur lui a donné un nouvel élan. En 1949, 2000
décimales étaient calculées par un des premiers
ordinateurs. En 1997, après 10 heures de calcul par 1024 processeurs
montés en parallèle, Yasumasa Kanada a déterminé
51 milliards de décimales du nombre
ne date bien sûr pas d'aujourd'hui mais l'utilisation
de l'ordinateur lui a donné un nouvel élan. En 1949, 2000
décimales étaient calculées par un des premiers
ordinateurs. En 1997, après 10 heures de calcul par 1024 processeurs
montés en parallèle, Yasumasa Kanada a déterminé
51 milliards de décimales du nombre  .
.
Formules basées sur un développement en série.
Voici quelques formules permettant de calculer  avec plus
ou moins de vitesse.
avec plus
ou moins de vitesse.
Formule de Leonhard Euler (1707-1783)
 2= 6 * (1 + 1/22 + 1/32 + 1/42 + 1/52 ......)
2= 6 * (1 + 1/22 + 1/32 + 1/42 + 1/52 ......)
Développement en série de arctg x avec x=1
(W.Leibniz 1646-1716 ou James Gregory 1638- 1675)
 = 4 * (1 - 1/3 + 1/5 - 1/7 + 1/9 ......)
= 4 * (1 - 1/3 + 1/5 - 1/7 + 1/9 ......)
Développement en série de arctg x avec x=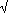 3/3 (Euler)
3/3 (Euler)
 = 2 *
= 2 * 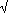 3 * (1 - 1/3 * 1/31 + 1/5 * 1/32 - 1/7 * 1/33 + ...)
3 * (1 - 1/3 * 1/31 + 1/5 * 1/32 - 1/7 * 1/33 + ...)
Formule de John Machin (1685-1751) à partir de arctg 1/5 - arctg 1/239
 = 16 * (1/51 - 1/3 * 1/53 + 1/5 * 1/55 - 1/7 * 57 + ...)
- 4 * (1/2391 - 1/3 * 1/2393 + 1/5 * 1/2395 - 1/7 * 1/2397 + ...)
= 16 * (1/51 - 1/3 * 1/53 + 1/5 * 1/55 - 1/7 * 57 + ...)
- 4 * (1/2391 - 1/3 * 1/2393 + 1/5 * 1/2395 - 1/7 * 1/2397 + ...)
Formule de John Wallis (1616-1703)
 = 2 * (2/1 * 2/3 * 4/3 * 4/5 * 6/5 * 6/7 * ...)
= 2 * (2/1 * 2/3 * 4/3 * 4/5 * 6/5 * 6/7 * ...)
Formule de François Viète (1540-1603)
2/ =
= 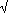 (1/2) *
(1/2) * 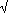 (1/2+1/2*
(1/2+1/2*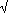 (1/2)) * ...
(1/2)) * ...
Formule de Brouncker (1620-1684)
4/ = 1+12/(2+32/(2+52/(2+72/.....)))
= 1+12/(2+32/(2+52/(2+72/.....)))
Voici les formules décrites ci-dessus mises en programme Pascal.
{$N+}
USES CRT;
VAR S, Err, P, Q, r : EXTENDED;
i : LONGINT;
Signe : SHORTINT;
BEGIN
CLRSCR;
{============================================================================}
S:=0;i:=0;Err:=1;
WHILE NOT (Err<1E-8) DO
BEGIN
INC(i);
Err:=1/i/i;
S:=S+Err
END;
S:=SQRT(S*6);
WRITELN('Par la formule de Euler (',i,' termes): ',S:9:7);
{============================================================================}
S:=0;i:=-1;Err:=1;Signe:=-1;
WHILE NOT (Err<1E-6) DO
BEGIN
INC(i,2);
Err:=1/i;
Signe:=-Signe;
S:=S+Err*Signe;
END;
WRITELN('Par le développement en série de arctg x avec x=1 (',i DIV 2,' termes): ',4*S:9:7);
{============================================================================}
S:=0;i:=-1;P:=3;Err:=1;Signe:=-1;
WHILE NOT (Err<1E-8) DO
BEGIN
INC(i,2);
P:=P/3;
Err:=P/i;
Signe:=-Signe;
S:=S+Err*Signe;
END;
WRITELN('Par le développement en série de arctg x avec x='+#251+'3/3 (',i DIV 2,' termes): ',2*SQRT(3)*S:9:7);
{============================================================================}
S:=0;i:=-1;P:=16*5;Q:=4*239;Err:=1;Signe:=-1;
WHILE NOT (ABS(Err)<1E-8) DO
BEGIN
INC(i,2);
P:=P/5/5;Q:=Q/239/239;
Err:=(P-Q)/i;
Signe:=-Signe;
S:=S+Err*Signe;
END;
WRITELN('Par la formule de John Machin (',i,' termes): ',S:9:7);
{============================================================================}
S:=1;i:=0;Err:=1;
WHILE NOT (Err<1E-8) DO
BEGIN
INC(i,2);
r:=i/(i-1)*i/(i+1);
Err:=ABS(S*r-S);
S:=S*r
END;
WRITELN('Par la formule de Wallis (',i DIV 2,' termes): ',2*S:9:7);
{============================================================================}
Err:=1;i:=0;r:=SQRT(1/2);S:=r;
WHILE NOT (Err<1E-8) DO
BEGIN
INC(i);
r:=SQRT(r/2+1/2);
Err:=ABS(2/S/r-2/S);
S:=S*r
END;
WRITELN('Par la formule de Viète (',i,' termes): ',2/S:9:7);
END.
Méthode de Monte-Carlo.
Des méthodes autres que géométriques ou analytiques ont été utilisées
pour déterminer une valeur de  . Par exemple les méthodes statistiques avec
lesquelles, la précision n'est pas obligatoirement au rendez-vous.
Il y a par exemple la méthode appelée "l'aiguille de Buffon" qui consiste
en le lâcher au-dessus d'une grille de lignes parallèles distantes d'une
unité de longueur. La probabilité que l'aiguille touche une des lignes est
de 2k/
. Par exemple les méthodes statistiques avec
lesquelles, la précision n'est pas obligatoirement au rendez-vous.
Il y a par exemple la méthode appelée "l'aiguille de Buffon" qui consiste
en le lâcher au-dessus d'une grille de lignes parallèles distantes d'une
unité de longueur. La probabilité que l'aiguille touche une des lignes est
de 2k/ où k est la longueur de l'aiguille.
Lazzerini affirma avoir utilisé cette méthode en 1901 pour trouver, à
l'aide de 34080 lancers, la valeur de 355/113 = 3,1415929
où k est la longueur de l'aiguille.
Lazzerini affirma avoir utilisé cette méthode en 1901 pour trouver, à
l'aide de 34080 lancers, la valeur de 355/113 = 3,1415929
Voici une autre méthode statistique basée sur une propriété géométique.
Traçons un carré dont le demi-côté mesure une unité
et inscrivons-y un cercle de rayon unitaire. La surface du carré est de 4
et celle du cercle est de  . Si vous choisissons au hasard
un point du carré, la probabilité qu'il se trouve dans le cercle est
de
. Si vous choisissons au hasard
un point du carré, la probabilité qu'il se trouve dans le cercle est
de  /4. Et par conséquent, en recommençant de plus
en plus souvent le choix aléatoire d'un point du carré, le
rapport entre le nombre de points se trouvant dans le cercle (dont la distance
à l'origine est inférieure à 1) et le nombre de points choisis
doit s'approcher de
/4. Et par conséquent, en recommençant de plus
en plus souvent le choix aléatoire d'un point du carré, le
rapport entre le nombre de points se trouvant dans le cercle (dont la distance
à l'origine est inférieure à 1) et le nombre de points choisis
doit s'approcher de  .
.
Les deux programmes ci-dessous réalisent l'implémentation de cette
méthode en mode texte et avec une visualisation graphique.
PROGRAM Monte_Carlo_Mode_Texte;
USES CRT;
VAR Cpt, {Cpt compte les lancers}
CptIn : LONGINT; {CptIn compte les coups dans la cible}
x, y : REAL; {Le point choisi au hasard}
BEGIN
TEXTCOLOR(YELLOW); {Texte en jaune}
TEXTBACKGROUND(RED); {Fond en rouge}
CLRSCR; {Efface l'écran}
CptIn:=0;Cpt:=0; {Initialise les compteurs}
WHILE NOT (KEYPRESSED OR (Cpt=MaxLongInt)) DO
BEGIN {Cpt=MaxLongInt évite que Cpt ne devienne trop grand}
x:=RANDOM; {Choix au hasard de x dans [0,1[}
y:=RANDOM; {Choix au hasard de y dans [0,1[}
INC(Cpt); {Un point de plus}
IF x*x+y*y<1 THEN INC(CptIn); {Point appartient au quart de cercle --> CptIn+1}
GOTOXY(36,13); {Amène le curseur en colonne 36 ligne 13}
WRITE('pi = ',4*(CptIn/Cpt):9:7); {Affiche pi}
END;
END.
PROGRAM Monte_Carlo_Graphique;
USES CRT,GRAPH;
VAR grDriver, grMode, ErrCode : INTEGER; {Paramètres graphiques}
x, y, r, xp, yp : WORD; {Coordonnées des points}
Cpt, {Cpt compte les lancers}
CptIn : LONGINT; {CptIn compte les coups dans la cible}
Dx, Dy : REAL;
S : STRING[20]; {Pour convertir pi en chaîne de caractères}
BEGIN
grDriver := Detect; {Détecte les paramètres du PC}
INITGRAPH(grDriver, grMode,''); {Initialise le mode graphique}
ErrCode := GraphResult; {Erreur à l'initialisation graphique?}
IF ErrCode<>grOk THEN WRITELN('Erreur ', GraphErrorMsg(ErrCode),' à l''initialisation graphique.')
ELSE BEGIN
x:=200;y:=400;r:=400;
DIRECTVIDEO:=FALSE;
SETCOLOR(YELLOW); {Affichage en couleur jaune}
CLEARDEVICE; {Efface l'écran en mode graphique}
SETFILLSTYLE(EmptyFill,BLACK); {Paramètres pour BAR}
SETTEXTSTYLE(SmallFont, VertDir, 1); {Paramètres d'affichage du texte}
RECTANGLE(x,y-r,x+r,y); {Dessine le carré de côté r}
ARC(x, y-r, 270, 360, r); {Dessine l'arc de cercle de rayon r}
CptIn:=0;Cpt:=0; {Initialise les compteurs}
WHILE NOT (KEYPRESSED OR (Cpt=MaxLongInt)) DO
BEGIN {Cpt=MaxLongInt évite que Cpt ne devienne trop grand}
Dx:=RANDOM; {Choix au hasard de Dx dans [0,1[}
Dy:=RANDOM; {Choix au hasard de Dy dans [0,1[}
xp:=x+TRUNC(Dx*r); {x du point trouvé au hasard}
yp:=y-r+TRUNC(Dy*r); {y du point trouvé au hasard}
INC(Cpt); {Un point de plus}
IF Dx*Dx+Dy*Dy<1 THEN BEGIN {Ce point appartient-il au quart de cercle?}
INC(CptIn); {On augmente le compteur}
PUTPIXEL(xp,yp,LIGHTGREEN); {Affiche le point}
END
ELSE PUTPIXEL(xp,yp,LIGHTRED); {Affiche le point en rouge clair}
GOTOXY(6,25); {Amène le curseur en colonne 6 ligne 25}
WRITE('ã = ',4*(CptIn/Cpt):9:7); {Affiche pi en mode texte}
STR(4*(CptIn/Cpt):9:7,S); {Transforme 4*(CptIn/Cpt) en texte}
BAR(100-TEXTHEIGHT(S),100,100,100+TEXTWIDTH(S)); {Efface l'ancien pi}
SETCOLOR(LIGHTBLUE); {Affichage en couleur jaune}
OUTTEXTXY(100,100,'pi = '+S); {Affiche pi en mode graphique}
END;
READKEY; {Attend qu'une touche soit enfoncée}
CLOSEGRAPH; {Quitte le mode graphique}
END;
END.
Autre méthode.
Voici une autre méthode pour calculer des valeurs approchées de  :
:
Placer d'abord les nombres 1, 2, 3, ... dans un tableau.
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
12 |
13 |
14 |
15 |
... |
... |
Etape 1: En commençant en 3ème position, supprimer tous les 2èmes éléments
Ceci donne:
1 |
2 |
4 |
6 |
8 |
10 |
12 |
14 |
16 |
18 |
20 |
22 |
24 |
26 |
28 |
... |
... |
Etape 2: En commençant en 5ème position, supprimer tous les 3èmes éléments
Ceci donne:
1 |
2 |
4 |
6 |
10 |
12 |
16 |
18 |
22 |
24 |
28 |
30 |
34 |
36 |
40 |
... |
... |
Etape 3: En commençant en 7ème position, supprimer tous les 4èmes éléments
Ceci donne:
1 |
2 |
4 |
6 |
10 |
12 |
18 |
22 |
24 |
30 |
34 |
36 |
... |
... |
…
En général, à la kème étape, il faut supprimer, en commençant à la (2k+1)ème position, tous les (k+1)èmes éléments.
On se retrouve ainsi avec:
1 |
2 |
4 |
6 |
10 |
12 |
18 |
22 |
34 |
42 |
48 |
58 |
... |
... |
Considèrons que la valeur de l'élément est fonction de sa position, on a f(n)=Tabn
Ex: f(1)=1; f(2)=2; f(3)=4; f(4)=6; f(5)=10; f(6)=12; f(7)=18; …
Le quotient n²/f(n) s'approche de Pi avec n croissant.
Ex: 1/1=1; 4/2=2; 9/4=2,25; 16/6=2,66666; 25/10=2,5; 36/12=3; 49/18=2.7222; 64/22=2,90900;81/30=2.7;100/34=2,94117;…
Notes:
1) cet algorithme apparaît dans le livre de Sloane "Handbook of Integer Functions" qui se réfère à un article de Yosef David dans le volume 11 de "Riveon Lematematika" (1957). Dans celui-ci, il était fait état que Jabotinski et Erdos avaient prouvé que f(n)=n^2/pi+O(n^(4/3)).
2) Kevin Brown a montré que la valeur de f(n) peut aussi être calculée en faisant:
déterminer le plus petit multiple de (n-1) supérieur ou égal à n
déterminer le plus petit multiple de (n-2) supérieur ou égal au nombre trouvé à l'étape précédente
…
déterminer le plus petit multiple de 1 supérieur ou égal au nombre trouvé à l'étape précédente
Exemple avec n=11:
le plus petit multiple de 10=(11-1) ³ 11 est 10* 2=20
le plus petit multiple de 9=(11-2) ³ 20 est 9* 3=27
le plus petit multiple de 8=(11-3) ³ 27 est 8* 4=32
le plus petit multiple de 7=(11-4) ³ 32 est 7* 5=35
le plus petit multiple de 6=(11-5) ³ 35 est 6* 6=36
le plus petit multiple de 5=(11-6) ³ 36 est 5* 8=40
le plus petit multiple de 4=(11-7) ³ 40 est 4*10=40
le plus petit multiple de 3=(11-8) ³ 40 est 3*14=42
le plus petit multiple de 2=(11-9) ³ 42 est 2*21=42
le plus petit multiple de 1=(11-10)³ 42 est 1*42=42
et on retouve bien f(11)=42 comme dans le tableau fabriqué ci-dessus.
Voici l'algorithme en Pascal. Pour rester le plus compréhensible possible, il n'a pas été optimisé.
PROGRAM Cl_Pi;
USES CRT;
FUNCTION F(n:LONGINT):LONGINT;
VAR i,M,x:LONGINT;
BEGIN
M:=n;
FOR i:=n-1 DOWNTO 1 DO
BEGIN
x:=i;
WHILE NOT (x>=M) DO x:=x+i;
M:=x;
END;
F:=M
END;
VAR i:LONGINT;
Xa,Xn:REAL;
BEGIN
Xa:=99;Xn:=0;i:=1;
WHILE NOT ((ABS(Xa-Xn)<1E-8) OR (i=2000)) DO
BEGIN
INC(i);
Xa:=Xn;
Xn:=i*i/f(i);
WRITELN(i:3,'²/',f(i):6,'=',Xn:12:9);
END;
END.
Formule basée sur les moyennes arithmétique et géométrique.
Voici la formule découverte par Eugène Salamin et Richard Brent en 1976 (Mathématics of computation).
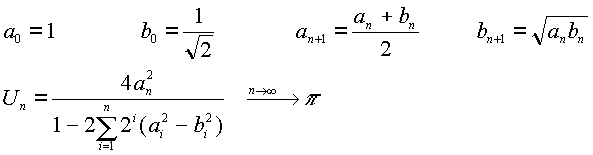
PROGRAM Pi_Salamin_Brent;
VAR S_Carr,Puiss2,a,b,an,bn,U,Un,Eps:DOUBLE;
BEGIN
Eps:=1E-6;
S_Carr:=0;Puiss2:=1;
an:=1;bn:=1/SQRT(2);
Puiss2:=1;
U:=1;Un:=0;
WHILE NOT (ABS(U-Un)<Eps) DO
BEGIN
a:=an;b:=bn;U:=Un;
an:=(a+b)/2;bn:=SQRT(a*b);
Puiss2:=Puiss2*2;
S_Carr:=S_Carr+Puiss2*(an*an-bn*bn);
Un:=4*an*an/(1-2*S_Carr);
END;
WRITELN('pi=',Un:16:14);
END.
Formule de David Bailey, Peter Borwein et Simon Plouffe.
David Bailey, Peter Borwein et Simon Plouffe viennent de découvrir un moyen de calculer la ième décimale de Pi sans
nécessiter la connaissance des décimales précédentes. Seul petit inconvénient: le chiffre trouvé est celui de la représentation
hexadécimale de Pi.
Voici la formule:
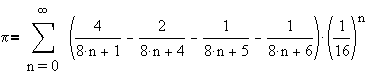
qui n'est qu'un cas particulier de la formule de Victor Adamchik et Stan Wagon parue dans un article de
American Math. Monthly n° 104 (1997)
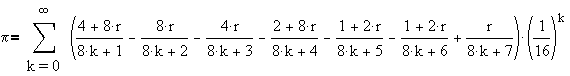
où r est n'importe quel nombre réel ou complexe.
Voici une implémentation de cet algorithme qui réalise le calcul de 101 chiffres de la représentation hexadécimale de Pi.
Pour comprendre comment calculer directement la ième chiffre de la représentation hexadécimale de Pi, je vous conseille de consulter la page suivante
PROGRAM Pi_Bailey_Borwein_Plouffe;
CONST Chiffres:STRING='0123456789ABCDEF';
VAR i,N,Chiffre_16:LONGINT;
S:REAL;
Pi_16:STRING;
BEGIN
N:=0;
S:=4-2/4-1/5-1/6;
Chiffre_16:=TRUNC(S);
Pi_16:=Chiffres[1+Chiffre_16]+',';
FOR i:=1 TO 100 DO
BEGIN
N:=N+8;
S:=(S-Chiffre_16)*16;
S:=S+4/(N+1)-2/(N+4)-1/(N+5)-1/(N+6);
Chiffre_16:=TRUNC(S);
Pi_16:=Pi_16+Chiffres[1+Chiffre_16];
END;
WRITELN('Pi en base 16=',Pi_16);
END.
Le nombre  a un site Internet
The
Uselessness of Pi and its irrational friends qui lui est dédié
et d'où proviennent certaines des information reprises sur cette page.
Visitez-le. Vous y découvrirez un tas de renseignements passionnants.
a un site Internet
The
Uselessness of Pi and its irrational friends qui lui est dédié
et d'où proviennent certaines des information reprises sur cette page.
Visitez-le. Vous y découvrirez un tas de renseignements passionnants.
Page précédente.
Page d'accueil.
 est à beaucoup de titres
un nombre magique et depuis plus de 4 mille ans, il exacerbe la curiosité
des mathématiciens.
est à beaucoup de titres
un nombre magique et depuis plus de 4 mille ans, il exacerbe la curiosité
des mathématiciens. n'apparaît qu'au XVIIe siècle
et l'usage de la lettre grecque qui commence avec le gallois William Jones
en 1706 (il lui attribue la valeur 3,14159) ne se répandra vraiment
qu'après avoir été employée par Euler en
1737.
n'apparaît qu'au XVIIe siècle
et l'usage de la lettre grecque qui commence avec le gallois William Jones
en 1706 (il lui attribue la valeur 3,14159) ne se répandra vraiment
qu'après avoir été employée par Euler en
1737.
, e et i ont droit à une lettre pour les représenter. A titre indicatif, il est amusant de souligner la relation 1+ei
=0 qui unit ces 3 nombres.
 se trouve dans
une liste de spécifications concernant la construction du temple de
Salomon, aux environs de 950 avant J.C. et elle vaut 3. Cette valeur manque
évidemment de précision mais du temps des Egyptiens et
Mésopotamiens, de meilleures estimations avaient déjà
cours, à savoir 25/8 = 3,125 et
se trouve dans
une liste de spécifications concernant la construction du temple de
Salomon, aux environs de 950 avant J.C. et elle vaut 3. Cette valeur manque
évidemment de précision mais du temps des Egyptiens et
Mésopotamiens, de meilleures estimations avaient déjà
cours, à savoir 25/8 = 3,125 et
![]() 10 = 3,162. On
retrouve aussi trace de rapport circonférence/diamètre
dans la Bible où on lui attribue la valeur 3.
10 = 3,162. On
retrouve aussi trace de rapport circonférence/diamètre
dans la Bible où on lui attribue la valeur 3.
 la valeur de
256/81=4*(1-1/9)2=3,16049...
la valeur de
256/81=4*(1-1/9)2=3,16049... n'apparaissait pas telle qu'écrite ci-dessus puisque les expressions algébriques étaient inconnues et que toute technique de résolution était exprimée en langage habituel. Cette expression est la déduction d'une règle permettant de calculer l'aire d'un cercle à partir de son rayon.
 <22/7.
Avec l'affinement des techniques de calcul mais en se basant toujours sur
l'encadrement d'Archimède, Ptolémée trouva au IIe
siécle après J.C. la valeur sexagésimale
3+8/60+30/3600=3,141666... Vers 500, Aryabhatta utilise 62832/2000=3,1416.
Au XVIe siècle, 30 décimales sont connues, 140 au
XVIIIe et 707 par Shanks à la fin du XIXe
(mais plus de 200 étaient fausses).
<22/7.
Avec l'affinement des techniques de calcul mais en se basant toujours sur
l'encadrement d'Archimède, Ptolémée trouva au IIe
siécle après J.C. la valeur sexagésimale
3+8/60+30/3600=3,141666... Vers 500, Aryabhatta utilise 62832/2000=3,1416.
Au XVIe siècle, 30 décimales sont connues, 140 au
XVIIIe et 707 par Shanks à la fin du XIXe
(mais plus de 200 étaient fausses).
 ne date bien sûr pas d'aujourd'hui mais l'utilisation
de l'ordinateur lui a donné un nouvel élan. En 1949, 2000
décimales étaient calculées par un des premiers
ordinateurs. En 1997, après 10 heures de calcul par 1024 processeurs
montés en parallèle, Yasumasa Kanada a déterminé
51 milliards de décimales du nombre
ne date bien sûr pas d'aujourd'hui mais l'utilisation
de l'ordinateur lui a donné un nouvel élan. En 1949, 2000
décimales étaient calculées par un des premiers
ordinateurs. En 1997, après 10 heures de calcul par 1024 processeurs
montés en parallèle, Yasumasa Kanada a déterminé
51 milliards de décimales du nombre  .
.
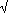 3/3 (Euler)
3/3 (Euler)