Flocon de von Koch.

En 1904, Helge von Koch (1870-1924 - Suède) publie l'article : « Sur une courbe continue sans tangente, obtenue par une construction géométrique élémentaire » qui décrit la ligne actuellement connue sous le nom de 'flocon de von Koch'.

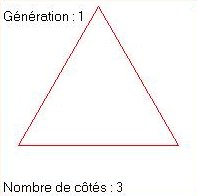
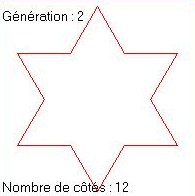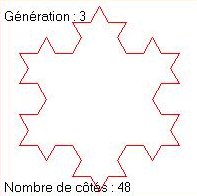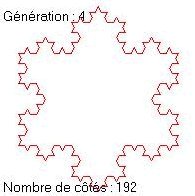La méthode.

Pour tracer cette courbe, il faut:

Tracez un triangle équilatéral
Remplacer le tiers central de chaque côté par une pointe dont la longueur de chaque côté égale aussi au tiers du côté
Recommencer cette construction sur chaque côté des triangles ainsi formés.

Un peu d'aide.

Reprenons la construction de la première étape:

Si on considère que les points a et b ont pour coordonnées (x_a,y_a) et (x_b,y_b), nous obtenons:

le point c (fin du premier tiers de ab) a pour coordonnées:
```
(x_a+(x_b-x_a)/3,
 y_a+(y_b-y_a)/3)
```
le point d (fin du deuxième tiers de ab) a pour coordonnées:
```
(x_a+2*(x_b-x_a)/3,
 y_a+2*(y_b-y_a)/3)
```
le point e (sommet du triangle construit sur le tiers central de ab) a pour coordonnées:
```
((x_c+x_d)*cos 60°-(y_d-y_c)*sin 60°,
 (y_c+y_d)*cos 60°+(x_d-x_c)*sin 60°)
```

Comment faire?

Pour la mise en oeuvre de l'algorithme, on peut utiliser plusieurs techniques dont:

mémoriser les points du premier triangle P₀,P₁,P₂ puis insérer les nouveaux points (en décalant donc les points existants).
Après la première étape, on obtient ainsi:
```
P₀,P₁,P₂,P₃,P₄ (l'ancien P₁),P₅,P₆,P₇,P₈ (l'ancien P₂),...,P₁₂ (l'ancien P₃)
```
Ces points peuvent être mémorisés dans un tableau ou dans une liste chaînée plus appropriée à des insertions/suppressions.

utiliser la récursivité:

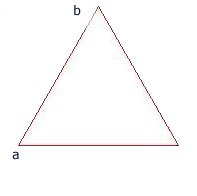
Dessiner(a,b,n) a et b déterminent le segment sur lequel doit être dessiné le triangle
aller en a
si n=0 alors tracer jusqu'en b il n'y a plus de triangle à générer et on trace
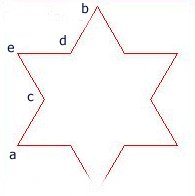
sinon on ne doit pas encore tracer et on va construire le niveau suivant sur les segments ac,ce,ed,db
      déterminer c point au tiers de ab
      déterminer d point au deux tiers de ab
      déterminer e sommet du triangle généré sur le tiers central de ab
      on va passer aux segments ac,ce,ed,db en indiquant le changement de niveau
      dessiner(a,c,n-1) on fait la même chose sur ac (premier tiers)
      dessiner(c,e,n-1) on fait la même chose sur ce (1er cote du triangle généré)
      dessiner(e,d,n-1) on fait la même chose sur ed (2ème cote du triangle généré)
      dessiner(d,b,n-1) on fait la même chose sur ab (dernier tiers)
fsi

Notes.

Le flocon de von Koch a des longueurs successives de:

état initial: L₁ = 3 * L (3 côtés de longueur L)
état 1:  L₂ = 3 * 4 * (L/3) = L₁ * 4/3 (12 côtés de longueur L/3)
état 2:  L₃ = 3 * 4 * 4 * (L/9) = L₂ * 4/3  (48 côtés de longueur L/9)
....

Cette longueur tend donc vers l'infini puisque multipliée à chaque étape par 4/3>1. De plus, chacun de ses points devient un point anguleux et donc la dérivée n'y existe pas. On se trouve ainsi en présence d'une courbe de longueur infinie et 'dérivable nulle part', délimitant une surface finie (inférieure à celle du cercle circonscrit au triangle initial).

Les implémentations en Delphi.

Cliquez ici pour charger la version avec tableau.
Cliquez ici pour charger la version avec liste chaînée.
Cliquez ici pour charger la version récursive.
Cliquez ici pour charger une version récursive avec 'interpréteur de commande' (tortue graphique).

Page précédente.
Page d'accueil.