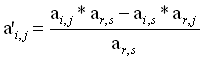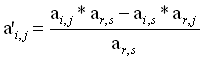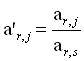Méthode de Gauss-Jordan.

Il existe de nombreuses méthodes de résolution de systèmes d'équations linéaires (LU, Crout, ... et Cramer, Gauss, substitution pour citer celles étudiées à l'école) mais la plus pratique est celle due à Gauss. Elle porte aussi le nom de méthode 'combili' qui décrit bien son mode de fonctionnement.

Cette méthode a l'avantage de pouvoir être aussi utilisée pour inverser une matrice et calculer un déterminant.

La méthode de Gauss-Jordan est basée sur la transformation de la matrice des coefficients des inconnues en une matrice unitaire par des combinaisons linéaires successives des différentes équations. A chaque étape, un coefficient (appelé pivot) d'une inconnue est choisi dans une équation et par un choix judicieux des coefficients multiplicatifs, l'algorithme fait apparaître des zéros dans la colonne de cette inconnue et un 1 à la place du pivot. Pour diminuer les erreurs d'arrondi, on choisit comme pivot l'élément le plus grand en valeur absolue se trouvant dans une ligne et une colonne dans lesquels aucun pivot précédent n'a été trouvé.

Soit donc le système à résoudre:
a1,1 x1 + a1,2 x2 + ... + a1,j xj + ....  + a1,n xn = a1,n+1
.....
ai,1 x1 + ai,2 x2 + ... + ai,j xj + ....  + ai,n xn = ai,n+1
.....
an,1 x1 + an,2 x2 + ... + an,j xj + ....  + an,n xn = an,n+1
qui en fin de processus sera devenu: 
1 x1 + 0 x2 + ... + 0 xj + ....  + 0 xn = a'1,n+1
0 x1 + 1 x2 + ... + 0 xj + ....  + 0 xn = a'i,n+1
.....
0 x1 + 0 x2 + ... + 1 xj + ....  + 0 xn = a'i,n+1
.....
0 x1 + 0 x2 + ... + 0 xj + ....  + 1 xn = a'n,n+1
Et il suffit de tirer la conclusion: 
x1 = a'1,n+1
x2 = a'2,n+1
.....
xj = a'j,n+1
....
xn = a'n,n+1
Note: seul petit inconvénient: le choix d'un pivot qui n'est pas systématiquement en positions (1,1), (2,2), ...., (n,n) fait qu'il faudra 'remettre' les équations dans le bon ordre pour lire les résultats.

Chaque étape (n au maximum puisqu'au mieux il est possible de trouver un pivot par ligne et colonne) commence par la recherche du pivot ar,s maximum en valeur absolue et appartenant à une ligne/colonne ne contenant pas un pivot déjà utilisé. Ensuite, tous les éléments de la matrice ai,j sont transformés par la règle dite du rectangle
avec r ¹ i = 1, ..., n et j = 1, ..., n+1 (1)
et les éléments de la ligne du pivot sont transformés par
avec j = 1, ..., n+1 (2)

Si lors d'une étape, le pivot vaut "zéro", le système est à déterminant nul et impossible à résoudre.

Le déterminant formé des coefficients des inconnues est calculé en faisant le produit des pivots multiplié par la valeur du déterminant formé des coefficients des inconnues en fin de processus; celui-ci vaut toujours +1 ou -1.

Pour l'inversion de la matrice des coefficients des inconnues, il faut compléter celle-ci par une matrice unité et appliquer les formules (1) et (2). En fin de processus, on affiche la matrice inverse en rétablissant l'ordre des lignes qui fait apparaître une matrice unité dans la partie qui contenait initialement les coefficients des inconnues.

Cliquez ici pour récupérer une archive contenant une implémentation en Delphi de la résolution d'un système d'équations linéaires, de l'inversion d'une matrice et du calcul d'un déterminant.
Ce programme pourrait être amélioré; ceci n'est qu'une version proche de l'algorithme pour être plus lisible.
Page précédente.
Page d'accueil.