Fibonacci.
Leonardo Pisano (1170 - 1250), fils de Guilielmo et membre de la famille Bonacci est plus connu sous le nom de Fibonacci. Ce fils de diplomate qui s'appelait lui-même parfois Bigollo (bon à rien ou voyageur) rédigeat le livre 'Liber abbaci' (1202) où il exploite ses connaissances en arithmétique accumulées lors de ses voyages (entre autres en Afrique du nord où il avait accompagné son père). Apparaît ainsi en Europe la notation décimale arabo-hindoue de position et l'usage des chiffres "arabes".

Entre autres, il découvrit que les carrés d'entiers pouvaient être générés en partant de 1 et en ajoutant successivement 3, 5, 7, 9, … aux nombres générés. 
Exemple: 1+3=4, 4+5=9, 9+7=16, 16+9=25 …
Autre découverte: pour déterminer un triple pythagoricien (x,y,z) tel que x²+y²=z², il remarqua qu'il suffisait de prendre pour x² n'importe quel carré impair et que y² était généré par la somme des nombres impairs inférieurs à x². 
Exemple: x²=49 et y²=1+3+5+7+..+47=(1+47)*24/2=24² et 49+576=625=25²
Mais Fibonacci est surtout connu par la suite qui porte son nom: 
F(0)=0, F(1)=1, F(2)=1, F(3)=2, F(4)=3, ..., F(i)=F(i-1)+F(i-2), ...
Cette suite est la solution au problème suivant posé par Fibonacci: supposons qu'un couple (mâle-femelle) de lapins immatures soit mis dans un champ, que la maturité sexuelle du lapin soit atteinte après un mois qui est aussi la durée de gestation, que chaque portée comporte toujours un mâle et une femelle et que les lapins ne meurent pas. Combien y aura-t-il de lapins dans le champ après un an? 
A la fin du 1er mois: 1 couple (le couple de départ C1)
à la fin du 2ème mois: 2 couples (C1 et les nouveaux-nés C2)
à la fin du 3ème mois: 3 couples (C1 et ses derniers nés: C3 + C2 à maturité)
à la fin du 4ème mois: 5 couples (C1 et ses derniers nés: C4 + C2 et ses derniers nés: C5 + C3 à maturité)
à la fin du 5ème mois: 8 couples (C1 et ses derniers nés: C6 + C2 et ses derniers nés: C7 + C3 et ses derniers nés: C8 + C4 et C5 à maturité)
…
Cette suite jouit de propriétés remarquables:

En calculant le quotient de 2 nombres consécutifs dans la suite de Fibonacci, on obtient une suite convergeant vers le nombre d'or (1+Ö5)/2: 
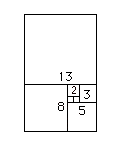
1/1=1, 2/1=2, 3/2=1.5, 5/3=1.666..., 8/5=1.6, 13/8=1.625, 21/13=1.61538...
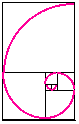
La suite de Fibonacci est aussi liée aux coquillages par le biais de la spirale logarithmique.

C'est le mathématicien français Edouard Lucas (1842-1891), qui donna le nom de nombres de Fibonacci à la suite 0, 1, 1, 2, 3, 5, 8, 13, … La suite des nombres qui portent son nom est calculée comme la suite de Fibonacci mais en prenant comme valeurs initiales les nombres 2 et 1.

Ces 2 suites sont liées par:

n: 0 1 2 3 4 5 6 7 8 7 10 ...
Fn: 0 1 1 2 3 5 8 13 21 34 55 ...
Ln: 2 1 3 4 7 11 18 29 47 76 123 ...
L(n) = F(n-1) + F(n+1) pour tous les entiers n
n: 0 1 2 3 4 5 6 7 8 7 10 ...
Fn: 0 1 1 2 3 5 8 13 21 34 55 ...
Ln: 2 1 3 4 7 11 18 29 47 76 123 ...
5 F(n) = L(n-1) + L(n+1) pour tous les entiers n
n: 0 1 2 3 4 5 6 7 8 7 10 ...
Fn: 0 1 1 2 3 5 8 13 21 34 55 ...
Ln: 2 1 3 4 7 11 18 29 47 76 123 ...
L(n) = F(n+2) - F(n-2) pour tous les entiers n
n: 0 1 2 3 4 5 6 7 8 7 10 ...
Fn: 0 1 1 2 3 5 8 13 21 34 55 ...
Ln: 2 1 3 4 7 11 18 29 47 76 123 ...
2 L(n) = F(n+3) + F(n-3) pour tous les entiers n

Les suites de Fibonacci sont aussi liées au triangle de Pascal dans lequel chaque ligne i est construite en plaçant 1 en colonne 1, en calculant les éléments des colonnes 2 à i par la somme de 2 nombres de la ligne précédente (celui placé au-dessus de lui et son prédécesseur) et en plaçant 1 en colonne i+1: 
   1    1
   1    2    1
   1    3    3    1
   1    4    6    4    1
   1    5   10   10    5    1
Avec 
   Ai,1 = 1
   Ai,j = Ai-1,j-1 + Ai-1,j pour j=2,...,i
   Ai,i+1 = 1
Si on présente le triangle de Pascal sous la forme suivante et qu'on calcule la somme des colonnes, on obtient les nombres de la suite de Fibonacci.

  0 1 2 3 4 5 6 7 8 9
0 1 . . . . . . . . .
1 . 1 1 . . . . . . .
2 . . 1 2 1 . . . . .
3 . . . 1 3 3 1 . . .
4 . . . . 1 4 6 4 1 .
5 . . . . . 1 5 10 10 5
6 . . . . . . 1 6 15 20
7 . . . . . . . 1 7 21
8 . . . . . . . . 1 8
9 . . . . . . . . . 1
F 1 1 2 3 5 8 13 21 34 55
L   1 3 4 7 11 18 29 47 76
Si nous refaisons la somme des nombres de chaque colonne mais en leur appliquant la formule 
       nbre*colonne/ligne.
Ainsi pour la colonne 4, nous obtenons, en partant de l'élément diagonal: 
       1*4/4 + 3*4/3 + 1*4/2 = 1 + 4 + 2 = 7
Cette fois nous avons obtenu les nombres de Lucas. 
entier N, a, b, c
écrire "Position du nombre de Fibonacci (N>2) ="
lire N
b ß 0
c ß 1
pour i de 3 à N faire
  a ß b
  b ß c
  c ß a+b
fpour
écrire "F(",N,")=",c

ou en utilisant un tableau à 3 éléments

entier N, i
tableau Tabi i=1,…,100 d'entier
écrire "Position du nombre de Fibonacci (N>2) ="
lire N
Tab1 ß 0
Tab2 ß 1
pour i de 3 à N faire
  Tab1+(i-1) mod 3 ß Tab1+(i-2) mod 3  + Tab1+(i-3) mod 3
fpour
écrire "F(",N,")=", Tab1+(i-1) mod 3
Page précédente.
Page d'accueil.