Exemple: 253 à diviser par 27
Ils établissaient certains multiples du dénominateur, en multipliant le nombre obtenu par 2, jusqu'à l'obtention d'un nombre supérieur au numérateur.
27 1 253
54 2 -216 (=8*27)
108 4 ----
216 8 37
512 16 -27 (=1*27)
----
10
On peut conclure que 253=10+(1*27)+(8*27)ou que 253/27=9+10/27
et 10/27 était exprimé sous la forme d'une somme de fractions à numérateur unitaire (seule exception: 2/3 était aussi accepté) et à dénominateur différents.
Donc: 253/27=9+1/3+1/27
C'est quoi les fractions égyptiennes?
On a tout naturellement donné le nom de 'fraction égyptienne' à la représentation d'une fraction sous la forme d'une somme de fractions à numérateurs unitaires.On ne sait pas très bien comment les égyptiens procédaient pour cette obtenir cette décomposition. Par contre, on sait que quand ils obtenaient une fraction du type 2/(pq) ils appliquaient la formule:
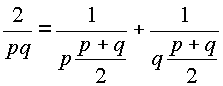
Intérêt des fractions égyptiennes de nos jours?
Les fractions égyptiennes rendent les comparaisons de fractions plus simples.Exemple: 3/4 est-il plus grand que 4/5?
Pour le savoir, nous passons à la représentation décimale (3/4=0,75<0,8=4/5) ou réduisons au même dénominateur (3/4=15/20<16/20=4/5).
En utilisant les fractions égyptiennes, la réponse est immédiate:
3/4 = 1/2 + 1/4 4/5 = 1/2 + 1/4 + 1/20
Autre avantage: imaginons que vous deviez partager 4 tartes entre 5 personnes. Il est évident que nous distribuerions des morceaux de tailles différentes à chacun mais dont la valeur totale serait chaque fois de 4/5ème de tarte. Ceci est juste d'un pont de vue mathématique mais risque sans doute de ne pas convaincre un enfant qu'il n'a pas reçu moins que son copain. Avec les fractions égyptiennes, chacun recevrait une moitié de tarte; laissant ainsi intacte une tarte et demie. De ce qui reste, on couperait des quarts qui seraient distribués à tous et finalement le quart restant serait divisé en 5 parts égales.
Remarques
Notons que la représentation sous forme d'une somme de fraction à numérateurs unitaires n'est pas unique. C'est pourquoi, ils avaient décidé d'utiliser celle contenant le moins de termes.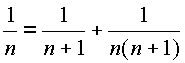
montre que la décomposition n'est pas unique.En 1201, Fibonacci (Leonard de Pise) prouva que tout nombre rationnel N/D pouvait s'écrire sous la forme d'une somme de fractions à numérateur unitaire et décrivit une méthode pour l'obtention des dénominateurs:
* si le nombre fractionnaire est supérieur à 1 (numérateur N supérieur au dénominateur D), on sépare la partie entière de la partie fractionnaire N'/D avec laquelle on travaillera; * si N'=1, la décomposition est terminée sinon on cherche la plus grande fraction 1/a inférieure ou égale à N'/D (donc le plus petit dénominateur a tel que 1/a est inférieur ou égal); * on recommence avec N'/D-1/a sauf si le nouveau numérateur est unitaire.
Le programme
1) on peut se passer de la séparation en partie entière et fractionnaire (en commençant avec a=1 et en acceptant que des numérateurs égaux tant que a=1);2) tout l'algorithme peut être implémenté sans utiliser la division.
3) dans le programme qui suit, il manque une simplification de la fraction obtenue à chaque étape
PROGRAM Egypt1;
VAR N,D,a:WORD;
Tmp:INTEGER;
BEGIN
WRITE('Num‚rateur = ');READLN(N);
WRITE('D‚nominateur = ');READLN(D);
WRITE(N,'/',D,'=');
a:=2;
Tmp=0;
WHILE (N>=D) DO
BEGIN
INC(Tmp);
N:=N-D;
END:
IF Tmp>0 THEN WRITE(Tmp);
a:=2;
WHILE NOT ((N=0) OR (a>200)) DO
BEGIN
Tmp:=a*N-D;
WHILE NOT (Tmp>=0) DO
BEGIN
INC(a);
Tmp:=a*N-D;
END;
WRITE('+1/',a);
N:=Tmp;D:=a*D;
INC(a); {évite d'avoir 2 fois le même dénominateur}
END;
END.