Distribution normale.

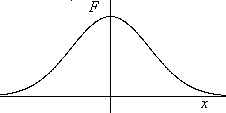
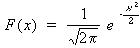
La loi normale ou loi de Gauss-Laplace est sans doute la loi de distribution de probablilité la plus connue. Voici son équation et sa célèbre représentation en cloche:



Elle a en fait été découverte par Moivre en 1738 comme limite de la loi binomiale.

Le calcul d'une probabilité passant par l'intégration de cette loi de distribution, nous sommes confrontés à l'absence de primitive de e-x²/2. L'intégration doit donc se faire avec d'autres techniques.
Une manière particulièrement efficace est de développer en série e-x²/2 et d'ensuite intégrer le développement.
Comme
ex=1 + x/1! + x2/2! + x3/3! + x4/4! + x5/5! + ...,

on a
e-x²/2=1 + (-x²/2)/1! + (-x²/2)2/2! + (-x²/2)3/3! + (-x²/2)4/4! + (-x²/2)5/5! + ...

dont l'intégration fournit:
x + (-x²/2)/1!*x/3 + (-x²/2)2/2!*x/5 + (-x²/2)3/3!*x/7 + (-x²/2)4/4!*x/9 + (-x²/2)(-x²/2)5/5!*x/11 + ...

Voici une implémentation en Pascal de cet algorithme: 
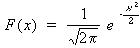
PROGRAM Dis_Normale;

VAR x,S,T,Fact:REAL;
    i:LONGINT;

BEGIN
WRITELN('Calcul de P(0,x) dans le cas d''une distibution normale.');
WRITE('x = ');READLN(x);
S:=x;
T:=x;
Fact:=-x*x/2;
i:=0;
WHILE NOT (ABS(T)<1E-6) DO
  BEGIN
  INC(i);
  T:=T*Fact*(2*i-1)/(2*i+1)/i;
  S:=S+T;
  END;
WRITELN('P(0≤x≤',x:5:3,')=',S/SQRT(2*Pi):9:7)
END.

Page précédente.

Page d'accueil.