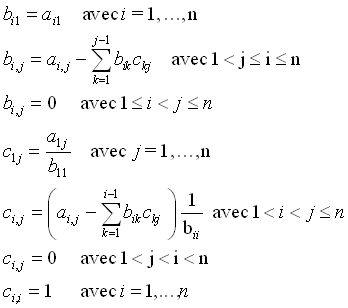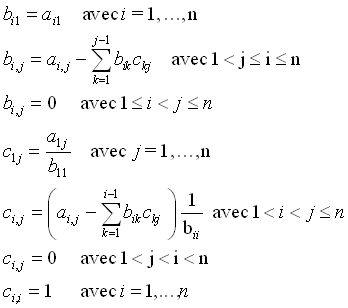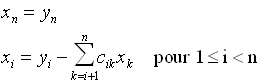Méthode de Crout.
La méthode de Crout propose de décomposer la matrice carrée
An x n en le produit LU où les éléments
bi,j de la matrice L et ci,j de la matrice U sont déterminés
grâce aux formules suivantes:
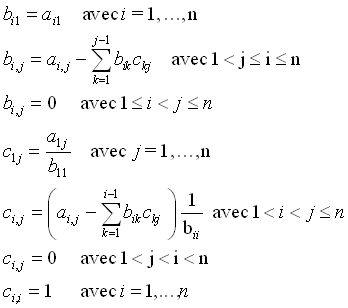
Le résultat de cette factorisation peut être utilisé pour la résolution
du système d’équations linéaires, écrit sous forme matricielle
A x = B. En général, les termes indépendants de ces équations
sont stockés dans une (n+1)ème colonne de la matrice A.
On a A x = B ó (LU) x = B ó L(U x) = B ó Ly = B avec y= U x
et la résolution se fait en 2 étapes:
ü
résolution de Ly = B grâce aux formules suivantes:
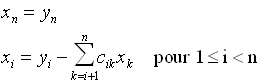 où ai,n+1 représente le terme indépendant de la ième équation
ü
résolution de Ux = y grâce aux formules suivantes:
où ai,n+1 représente le terme indépendant de la ième équation
ü
résolution de Ux = y grâce aux formules suivantes:

Notes:
Des divisions par bii apparaissant, il est possible que la méthode ne permette
pas de trouver la solution même si elle existe. Pour trouver une solution existante, il faudrait
changer l'ordre des équations; ce qui est un travail considérable pour trouver un arrangement qui
n'apporterait pas de bii nul.
Les matrices L et U étant triangulaires, elles peuvent être stockées dans un même tableau carré et
même mieux, elles peuvent être stockées dans A!
Cette méthode peut aussi être utilisée pour inverser une matrice, il suffit de résoudre les n systèmes
d'équations ayant successivement pour seconds membres: (1,0,0,...,0), (0,1,0,...,0), ..., (0,0,....,1).
Cliquez ici pour récupérer une archive contenant une implémentaion de la
méthode en Turbo Pascal. Vous y trouverez la décomposition dans 2 matrices L et U distinctes et
dans une seule matrice.
Page précédente.
Page d'accueil.